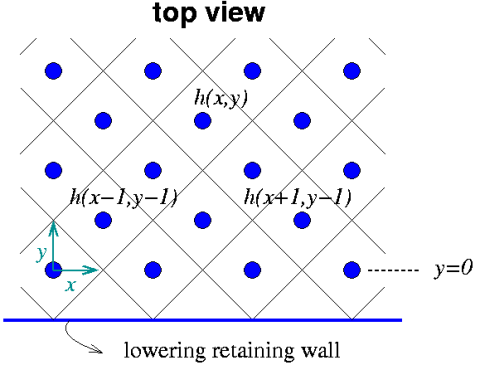
We define a lattice model to simulate this system. A height variable, h, is defined on a square lattice, (x, y), tilted at 45° meaning x is an odd (even) integer when y is an odd (even) integer.

We then define the stability condition as
and when the stability condition is violated, the toppling rule as
where 0<=\etai<=sc is a random number depends on the coordinate and avalanche index, i.
To simulate the slow lowering of the side wall, for each avalanche, indexed i, we trigger it by taking one of the highest sites on the bottom row, y=0, and reduce its height by a random amount, \etai . We then repeatedly topple all the unstable sites until the whole system is stable. Since the stability of a site depends only on its two bottom neighbors, we choose to update the system row by row from the bottom.
We call the sites topple in an avalanche the avalanche cluster and define the length and width of the avalanche to be the maximum difference in y and x coordinates of the toppling sites from the triggering point. The depth of an avalanche is defined as the maximum height change among the toppling sites while the mass is defined as the total height change of the whole avalanche cluster.